Understanding the central limit theorem (CLT) for businesses

The central limit theorem (CLT) is a crucial concept in statistics. It explains that when you take a large enough number of samples from any population, the distribution of the sample means will approach a normal distribution (bell curve), even if the original population distribution is not normal. This theorem is essential because it allows businesses to make accurate predictions and decisions based on sample data. For example, it helps understand customer behaviour, product quality, and financial risks by analysing samples instead of entire populations.

Formula of CLT

The central limit theorem relies on a specific formula:

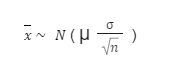
Here’s what each part means:

•  x Is the sample mean, the average of your sample data
• μ is the population mean, the average of the entire population.
• σ is the population standard deviation, which measures the spread of data points in the population.
• “n” is the sample size or the number of observations in your sample.

This formula shows that as the sample size n increases, the sample mean x will approximate a normal distribution centred around the population mean μ\muμ, with a spread (standard deviation) that decreases as the sample size grows. Understanding this formula helps businesses see why larger samples provide more accurate reflections of the population, enabling better decision-making based on sample data.

What are the three rules of the CLT?

To fully grasp the implications of the central limit theorem (CLT), it’s essential to understand its three fundamental rules:

Mean of the sampling distribution

The mean of the sample means is equal to the population mean. This means that if you repeatedly take random samples from a population and calculate the mean of each sample, the average of those sample means will equal the actual mean of the population.

Variance of the sampling distribution

The variance of the sample means decreases as the sample size increases. The variability among the sample means is minor when the sample size is more significant. This reduction in variability occurs because larger samples tend to provide a more accurate representation of the population.

The shape of the sampling distribution

The distribution of the sample means it approaches a normal distribution as the sample size increases. Regardless of the shape of the original population distribution, the distribution of the sample means will become approximately normal if the sample size is large enough (usually more than 30).

Why is 30 the minimum sample size?

A sample size of 30 is generally considered the minimum because it is often sufficient for the sample mean distribution to approximate a normal distribution, regardless of the population’s original distribution. This threshold helps in achieving more reliable and accurate inferences about the population.

Conditions for the central limit theorem

Certain conditions must be met for the central limit theorem to apply accurately. These conditions ensure that the sampling distribution will indeed approximate a normal distribution:

Large sample size

The sample size must be large, typically n≥30n \geq 30n≥30. Larger samples provide a better approximation of the population mean and ensure that the sampling distribution of the sample mean approaches normality.

Independence

Samples must be independent, meaning the selection of one sample does not influence the choice of another. This condition ensures that each sample is representative of the population and that the behaviour of one sample does not affect the others.

Finite variance

The population from which samples are drawn should have a finite variance. This condition ensures that the sample means will converge to a normal distribution as the sample size increases. The sample means may not form a normal distribution if the population variance is infinite.

Application in a business context

Understanding and applying the CLT is highly beneficial for various business applications. It provides a foundation for making accurate predictions and informed decisions based on sample data, which is crucial in different areas such as market research, quality control, and financial modelling.

Sampling and market research

Businesses use the central limit theorem to conclude a population from sample data. For instance, market researchers can estimate customer preferences by analysing a representative sample. This allows them to make accurate predictions about the larger market.

Quality control and manufacturing

In manufacturing, CLT helps with quality control by enabling businesses to monitor production processes through sample inspections. This ensures product consistency and quality without the need to check every single item.

Financial modelling and risk assessment

CLT is vital in financial modelling for estimating risks and returns. Businesses can model financial data to make informed investment decisions and effectively manage risks by analysing sample data from market behaviours.

Benefits of using CLT in business

Applying the central limit theorem in business offers several significant advantages. By understanding and utilising CLT, companies can make more precise predictions and informed decisions, improving operational efficiency and strategic planning.

Enhanced accuracy in statistical predictions

The central limit theorem helps businesses to draw accurate conclusions about a population from sample data. This improved accuracy is crucial for reliable market research, financial analysis, and quality control.

Improved decision-making processes

Businesses can make better-informed decisions with the insights gained from CLT. Whether forecasting sales, managing inventory, or assessing financial risks, the theorem provides a solid statistical foundation for decision-making.

Reduction of uncertainty in business operations

CLT reduces uncertainty in various business processes by providing a clearer understanding of population parameters from sample data. This leads to more predictable outcomes and better risk management, enhancing overall business stability and performance.

Challenges and considerations

While the central limit theorem is a powerful tool for business applications, it is essential to understand its limitations and the challenges involved in applying it effectively.

Importance of appropriate sample sizes

The accuracy of the central limit theorem depends on having a sufficiently large sample size. Small samples may need to represent the population, leading to accurate conclusions adequately.

Potential pitfalls and limitations

Businesses must be aware of the CLT assumptions, such as the need for independent and identically distributed samples. Violating these assumptions can result in misleading results.

Assumptions underlying the theorem

Understanding the assumptions of CLT, such as the requirement for large sample sizes and the normality of sample means, is crucial for accurate application in business contexts. Businesses must ensure these conditions are met to obtain reliable analysis outcomes.

Prospects and advancements with CLT

As businesses face emerging challenges, the future application of the central limit theorem (CLT) promises further advancements in strategic decision-making and overall performance by:

Adapting to big data for accurate predictions

CLT helps analyse large datasets, making accurate predictions and identifying trends. This enables businesses to adapt quickly to market changes and consumer preferences, enhancing their competitive edge.

Enhancing predictive analytics for better forecasts

Using CLT ensures that sample data is representative of the population, leading to more reliable forecasts. This improves business planning and decision-making, helping companies anticipate future trends and demands.

Improving machine learning models with representative samples

CLT ensures that samples used in training machine learning models accurately represent the population. This leads to more effective algorithms, enhancing customer segmentation and fraud detection tasks.

Optimising quality control processes through regular sampling

By applying CLT, businesses can monitor production quality efficiently through regular sampling. This ensures consistent product standards, reducing defects and enhancing customer satisfaction.

Facilitating risk management with accurate risk estimates

CLT provides accurate risk estimates based on sample data, aiding in better risk management. Businesses can prepare for potential risks more effectively, ensuring excellent stability and resilience in operations.

FAQs

What are the three properties of the central limit theorem?

• The mean of the sampling distribution of the sample means is equal to the population mean.
• The variance of the sampling distribution is the population variance divided by the sample size.
• As the sample size increases, the sampling distribution approaches a normal distribution.

What are the advantages of the central limit theorem? 

The CLT allows for accurate predictions and informed decision-making based on sample data, enhances accuracy in statistical predictions, improves decision-making processes, and reduces uncertainty in business operations.

What are the disadvantages of the central limit theorem? 

The CLT requires a sufficiently large sample size and independent samples with finite variance. Violating these conditions can lead to inaccurate conclusions.

What are the real-world applications of CLT? 

The CLT is used in market research, quality control, financial modelling, and risk assessment to make accurate predictions and informed decisions based on sample data.

Why is it called the central limit theorem? 

It describes the central role of the normal distribution in the theory of probability and statistics.