What drives business success? The answer often lies in the ability to make informed decisions. Understanding how different variables are interconnected is a powerful tool that helps in this process. Imagine knowing how one factor impacts another, allowing you to predict outcomes more accurately and plan strategically. This concept, commonly known as correlation, is not just theoretical; it’s practical and has real-world applications in various aspects of business.
What is a correlation?
In business, correlation refers to the relationship between two variables and how they move about each other. For instance, it helps companies understand how changes in consumer spending might affect sales revenue. By analyzing it, businesses can make informed decisions, identify trends, and anticipate potential risks or opportunities, ultimately guiding strategic planning and operational adjustments.

Understanding what correlation can reveal
Correlation indicates the strength and direction of a relationship between two variables, quantified by the correlation coefficient. This coefficient ranges from -1.0 to 1.0, where values closer to 1 or -1 suggest a stronger relationship.
A correlation of 1 represents a perfect positive correlation, meaning two variables move together in the same direction. In contrast, a correlation of -1 indicates a perfect negative correlation, meaning as one variable increases, the other decreases in a directly opposite pattern. A correlation of zero implies no linear relationship exists between the variables.
For example, large-cap mutual funds often show a strong positive correlation with the S&P 500 Index, meaning their movements closely align with this market benchmark. Small-cap stocks may also exhibit positive correlation with the S&P, but typically at a lower level.
In cases like put option contracts and their underlying stock prices, correlation turns negative. A put option gives the owner the right to sell a specific quantity of the stock at a set price within a particular timeframe.
When the stock price drops, the value of the put option rises, creating a high negative correlation. As the stock price increases, put options tend to decrease in value, underscoring the inverse relationship and how correlation can highlight both direction and strength in such asset interactions.
Types of correlation
In the business world, knowing how different variables correlate with one another can be crucial. Now let us learn about its various kinds:
Positive correlation
It refers to the fact that as one variable increases, the other also increases. For example, consider a company that notices that as its marketing spending increases, its sales also rise. This indicates a positive relationship between marketing expenditure and sales revenue. The more the company invests in marketing, the higher the sales figures.
Negative correlation
Conversely, a negative value occurs when one variable increases while the other decreases. For instance, a company might find customer satisfaction increases as defective products decrease. Here, there’s a negative relationship between product defects and customer satisfaction. Improving product quality (reducing defects) will likely enhance customer satisfaction.
Zero correlation
Sometimes, there might be no discernible connection between two variables, referred to as zero correlation. For example, a business might find no significant link between the number of social media posts and direct sales, suggesting that other factors influence sales more strongly. This indicates that changes in one variable do not predict changes in the other.
Correlation strength
The strength of a linear correlation between two variables reflects how closely they move together in a dataset. Measured using Pearson’s Correlation Coefficient, correlation values range from -1 to 1, with values near 0 indicating weaker correlations and values closer to -1 or 1 signaling stronger relationships. Weaker correlations, though less predictive, can still reveal valuable insights for strategic business decisions.
For instance, a weak correlation between high TV ad spend and sales does not mean the data lacks value. Instead, it may highlight an opportunity for improvement, such as reducing TV ad budgets to achieve cost savings without significantly impacting sales.

Measurement Of correlation
A clear measurement is crucial for identifying the relationship between two variables. The “correlation coefficient” is a simple way to show how closely two variables are connected.
What is the coefficient of correlation?
The correlation coefficient is a statistical measure that quantifies the strength and direction of the relationship between two variables.
Calculation
The most widely used correlation coefficient is the “Pearson correlation coefficient”. It measures the linear relationship between two variables. Here’s how to calculate it step-by-step:
- Gather paired data for the two variables you want to analyse.
- Compute the mean (average) for each variable.
- Subtract the variable’s mean from each value for each data pair to get the deviation scores.
- Multiply the deviation scores for each pair.
- Square each deviation score for both variables.
- Sum up all the products of the deviations and the squared deviations.
- Use the Pearson correlation coefficient formula:
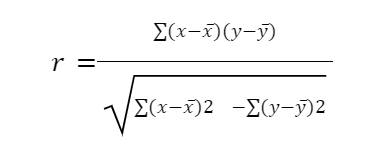
Where:
- r is the Pearson correlation coefficient
- X and Y are the two variables
- X̅ and Y̅ are the means of the variables
Interpretation
Once you’ve calculated the coefficient, interpreting it correctly is crucial for making informed business decisions.
| Correlation Coefficient Range | Description | Interpretation |
| +1 | Perfect positive value | Both variables increase proportionally. |
| -1 | Perfect negative value | One variable increases while the other decreases proportionally. |
| 0 | No correlation | There is no relationship between variables. |
| 0.7 to 0.9 (or -0.7 to -0.9) | Strong value | There is a significant relationship. Positive: An increase in one variable leads to a considerable increase in the other. Negative: A rise in one variable leads to a considerable decrease in the other. |
| 0.4 to 0.6 (or -0.4 to -0.6) | Moderate value | Noticeable relationship but not strong. |
| 0.1 to 0.3 (or -0.1 to -0.3) | Weak value | Weak relationship. |
Real-life example
The relationship between advertising spend and sales revenue is a practical illustration of the correlation in business. Let us say that the online retailer TechMart wants to know how its advertising spend affects sales. Over a number of months, TechMart has gathered information regarding its monthly advertising expenditure and related sales income. To maximise their marketing strategy, the objective is to ascertain whether there is a significant correlation between the two variables.
For six months, TechMart collects the following information:
| Month | Advertising Spend ($) | Sales Revenue ($) |
| January | 50,000 | 200,000 |
| February | 60,000 | 250,000 |
| March | 55,000 | 230,000 |
| April | 70,000 | 300,000 |
| May | 65,000 | 270,000 |
| June | 80,000 | 350,000 |
Calculations
- Calculate the mean values.
Mean advertising spend X = (50000 + 60000 + 55000 + 70000 + 65000 + 80000) / 6 = 64500
Mean Sales Revenue Y = (200000 + 250000 + 230000 + 300000 + 270000 + 350000) / 6 = 266666.67
- Calculate how much the advertising spend and monthly sales revenue differ from their averages.
- Multiply the differences for each month.
- Add up the products of the differences and the squared differences for both variables.
- Use the formula to find the correlation coefficient.
r=(x-x̅)(y-y̅)(x-x̅)2-(y-y̅)2
After the calculations, TechMart finds that the correlation coefficient (\(r\)) is approximately 0.95, indicating a strong positive correlation between advertising spend and sales revenue.
Interpretation
The correlation coefficient of 0.95 suggests that as TechMart increases its advertising spend, its sales revenue tends to increase significantly. This strong positive correlation means that the marketing efforts are effectively driving sales.
With this insight, TechMart can make informed decisions about future advertising budgets. For instance, if they plan to boost sales, they can confidently increase their advertising spend, anticipating a proportional increase in revenue. Additionally, they can experiment with different advertising channels and campaigns to further optimise their return on investment (ROI).
Importance of correlation in the business world
Understanding how different factors correlate can significantly enhance decision-making in various business areas. Here are some practical applications:
Analysis of market trends
Businesses frequently need to predict market trends to remain competitive. Companies can make more informed predictions by analysing how different market variables correlate. A fashion retailer, for instance, might investigate the relationship between sales patterns and seasonal trends. If they see a favourable relationship between particular seasons and rising demand for particular products, they can modify their inventory and marketing plans appropriately.
Risk management
In finance, understanding the relationship between different investments is crucial for managing risk. For example, a portfolio manager might analyze how the stock prices of various companies move in relation to each other. If two stocks tend to move in opposite directions, the manager might include both in the portfolio to balance risks. When the value of one stock decreases, the other might increase, providing a buffer against losses.
Improving operational efficiency
Businesses can also use this knowledge to enhance operational efficiency. For instance, a manufacturing company might analyze the relationship between machine maintenance frequency and production output. If they discover that increased maintenance leads to fewer breakdowns and higher output, they can optimize their maintenance schedules to improve productivity. This strategic adjustment ensures machines operate smoothly, maximizing production capabilities.

The benefits of correlation in decision making
Using correlation in decision-making enables businesses to analyze historical data and gain insights into the effectiveness of various initiatives, from marketing campaigns and product offerings to workplace efficiency. Correlation analysis provides a quantitative approach, complementing qualitative insights to create a more comprehensive decision-making strategy.
By assessing the relationship between initiatives and their outcomes, correlation helps companies identify patterns, evaluate what has worked well in the past, and adapt strategies accordingly. This approach uncovers hidden opportunities, sharpens focus, and supports better allocation of resources, leading to more informed, data-driven decisions and improved business performance.
Tools for analysing correlation
Businesses often use tools like correlation matrices to analyse and visualise these correlations. A correlation matrix displays the correlations between multiple variables in a grid format, making it easier to identify patterns.
Creating a correlation matrix
Let’s consider a company that wants to understand the relationship between various factors affecting its sales. They might include variables like advertising spend, product pricing, customer reviews, and seasonal trends. By inputting these variables into a correlation matrix, the company can easily see which factors have the strongest correlations with sales.
Interpreting the matrix
In the matrix, each cell represents the relationship between two variables. For example, if the cell showing the relationship between advertising spend and sales displays a value of 0.75, it indicates a strong positive relationship. Conversely, a value of -0.6 between product pricing and sales might suggest that higher prices are associated with lower sales. This format allows for quick, clear visualization of how different variables might affect each other, aiding in strategic planning and decision-making.
Limitations of correlation
While understanding relationships between variables is powerful, it’s important to recognize its limitations. One common pitfall is confusing correlation with causation. Just because two variables are closely related doesn’t mean one causes the other.
For example, a company might notice a strong positive relationship between ice cream and sunglasses sales. However, this doesn’t imply that buying sunglasses causes people to buy ice cream. The actual cause might be the summer season, which increases the demand for both products.
To avoid misinterpretation, it’s crucial to consider the context and look for underlying factors that might influence the relationship. Additionally, using other statistical methods and conducting experiments can help validate the findings.

FAQs
How does correlation help in making business decisions?
It helps businesses understand the relationship between different variables. By analysing these relationships, companies can predict outcomes, optimise strategies, and make informed decisions in areas such as marketing, risk management, and operational efficiency.
What steps are involved in calculating the correlation coefficient?
It involves gathering paired data, calculating the mean for each variable, computing deviations from the mean, multiplying these deviations, and then applying the Pearson formula. This results in a coefficient that indicates the strength and direction of the relationship.
What do different values of the correlation coefficient indicate?
A coefficient close to +1 indicates a strong positive value, where both variables increase together. A coefficient close to -1 indicates a strong negative value, where one variable increases as the other decreases. A coefficient around 0 indicates no correlation, meaning changes in one variable do not predict changes in the other.
Can a strong correlation between two variables imply that one causes the other?
No, a strong correlation does not imply causation. Two variables might strongly correlate due to a third underlying factor or purely by coincidence. It is important to conduct further analysis to determine if there is a causal relationship.
What are some common pitfalls to avoid when interpreting correlations?
Common pitfalls include confusing correlation with causation, ignoring the potential impact of outliers, and not considering the broader context. Additionally, relying solely on correlation without using other statistical methods can lead to incomplete or misleading conclusions.


